bzoj 1808: [Ioi2007]training 训练路径

.

题意：在一个图中，有一些边组成了一棵树，其他边都有个权值。你可以删除一些非树边使图中没有长度为偶数的环，问最小代价。
题解：LCA+DP
我们可以把题目转化为选一些边使权值最大。有个结论：最后一定是个仙人掌（一条边最多在一个环里）。那么我们可以状压DP来搞一下。f[i][j]表示已i为根的子树，属于集合j的儿子不考虑的最大权值和。官方题解的图讲的很清晰：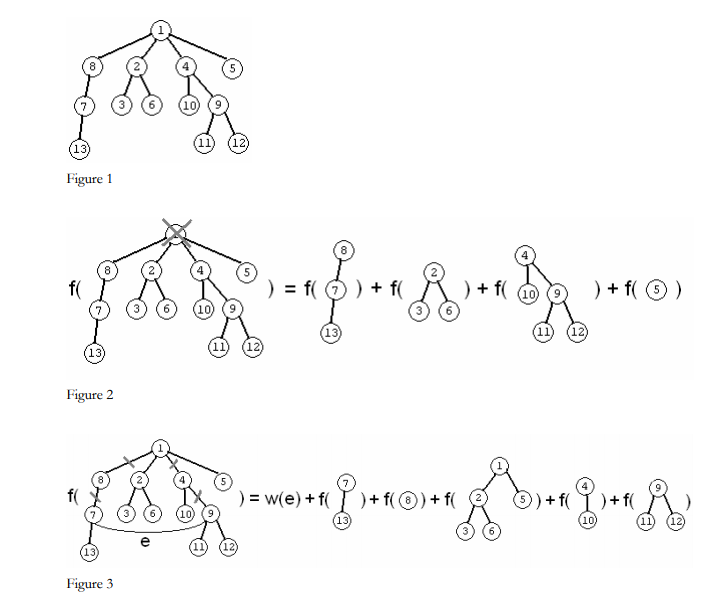
代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,num=0,fst[1010],nnum=0,sum=0,f[1010][1030],u[2010],sn[1010],vs[1010],nn;
struct edge
{
    int x,y,n;
}e[10010];
struct nte
{
    int x,y,c;
}ne[5010];
vector<int>ee[1010];//每个点是哪些非树边的lca
struct pnt
{
    int dep,f[12];
}p[2010];
void ins(int x,int y)
{
    e[++num]={x,y,fst[x]};
    fst[x]=num;
}
void pre(int x,int f)
{
    p[x].f[0]=f;
    p[x].dep=p[f].dep+1;
    for(int i=1;i<12;i++)
    p[x].f[i]=p[p[x].f[i-1]].f[i-1];
    for(int i=fst[x];i;i=e[i].n)
    {
        int y=e[i].y;
        if(y==f)
        continue;
        u[y]=1<<sn[x];
        sn[x]++;
        pre(y,x);
    }
    nn++;
    vs[x]=nn;
    u[nn]=0;
    p[nn].f[0]=x;
}
int lca(int x,int y)
{
    if(p[x].dep<p[y].dep)
    swap(x,y);
    for(int i=11;i>=0;i--)
    if((1<<i)<=p[x].dep-p[y].dep)
    x=p[x].f[i];
    if(x==y)
    return x;
    for(int i=11;i>=0;i--)
    if(p[x].f[i]!=p[y].f[i])
    {
        x=p[x].f[i];
        y=p[y].f[i];
    }
    return p[x].f[0];
}
void wk(int x)
{
    for(int i=fst[x];i;i=e[i].n)
    {
        int y=e[i].y;
        if(y==p[x].f[0])
        continue;
        wk(y);
    }
    for(int i=0;i<ee[x].size();i++)
    {
        nte e=ne[ee[x][i]];
//        printf("%d %d\n",e.x,e.y);
        int a,b,sum=e.c;
        for(a=vs[e.x];p[a].f[0]!=x;a=p[a].f[0])
        sum+=f[p[a].f[0]][u[a]];
        for(b=vs[e.y];p[b].f[0]!=x;b=p[b].f[0])
        sum+=f[p[b].f[0]][u[b]];
        for(int j=(1<<sn[x])-1;j>=0;j--)
        {
            if((j&u[a])==0&&(j&u[b])==0)
            f[x][j]=max(f[x][j],sum+f[x][j|u[a]|u[b]]);
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    nn=n;
    for(int i=0;i<m;i++)
    {
        int x,y,c;
        scanf("%d%d%d",&x,&y,&c);
        ne[++nnum]={x,y,c};
        sum+=c;
        if(!c)
        {
            ins(x,y);
            ins(y,x);
        }
    }
    pre(1,0);
    for(int i=1;i<=nnum;i++)
    {
        int hh=lca(ne[i].x,ne[i].y);
        if(!(p[ne[i].x].dep+p[ne[i].y].dep-(p[hh].dep<<1)&1)||ne[i].c==0)
        ee[hh].push_back(i);
    }
    wk(1);/*
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<(1<<sn[i]);j++)
        printf("%d ",f[i][j]);
        puts("");
    }*/
    printf("%d",sum-f[1][0]);
}